Ciągi de Bruijna drugiego rodzaju

Limit pamięci: 32 MB

Ciągiem de Bruijna rzędu nazywamy takie słowo złożone z znaków 0 i 1, że każde -literowe słowo złożone z zer i jedynek stanowi podsłowo, czyli spójny fragment, . Przykładem ciągu de Bruijna rzędu 3 jest 0001011100.

Ciągiem de Bruijna drugiego rodzaju rzędu nazywamy dowolnej długości takie słowo , że każde -literowe słowo złożone z zer i jedynek stanowi podciąg, czyli niekoniecznie spójny fragment, . Przykładem ciągu de Bruijna drugiego rodzaju rzędu 3 jest 00101101. Co prawda, o ile nam wiadomo, Nicolaas Govert de Bruijn już takich ciągów nie wymyślił, ale są one podobnie zdefiniowane do oryginalnych, nieprawdaż?

Załóżmy, że dany jest pewien zero-jedynkowy napis . Ile minimalnie cyfr (0 lub 1 oczywiście) należy do niego dokleić na końcu, tak aby stał się ciągiem de Bruijna drugiego rodzaju rzędu ?

Wejście

Pierwszy wiersz standardowego wejścia zawiera dwie liczby całkowite oraz (), oddzielone pojedynczym odstępem. Drugi wiersz zawiera 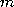-literowy napis złożony wyłącznie z cyfr 0 i 1, niezawierający żadnych odstępów.

Wyjście

Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą nieujemną, oznaczającą minimalną liczbę cyfr, jakie trzeba dokleić na koniec napisu , tak aby stał się c.d.B.d.r. rzędu .

Przykład

Dla danych wejściowych:

5 3
00101

poprawną odpowiedzią jest:

2

Wyjaśnienie do przykładu: Po dodaniu znaków 01 otrzymujemy następujący c.d.B.d.r. rzędu 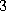: 0010101.

Autorzy zadania: Marek Cygan i Jakub Radoszewski.